Vysvětlení slovní úlohy o počítačové hře - hledám co nejjednodušší řešení
Prosím o nástin řešení pro žáky 5. třídy ZŠ: V počítačové hře se pohybuje celkem 50 koleček a 50 čtverečků. Jestliže se setkají čtyři kolečka se třemi čtverečky nebo tři kolečka se čtyřmi čtverečky, tak všech sedm útvarů zmizí. Cílem hry je nechat zmizet všechny čtverečky. Otázka: Jaký nejmenší a největší počet koleček může zbýt na konci hry, pokud zmizí všechny čtverečky? Děkuji.
Radka M.
26. 12. 2024 09:37
6 odpovědí
Naivny pristup by bol - najviac koliecok zostane, ak pouzijem strategiu parovania styri stvorceky a tri koliecka. Ale rychlo zistim, ze na konci mi zostanu dva stvorceky, ktore uz neviem nechat zmiznut \(4*12=48\).
Budem preto musiet hladat taku kombinaciu trojic a stvoric, ktora mi da dohromdy 50.
Oznacme pocet trojic \(T\) a pocet stvoric \(S\), potom musi platit:
\( 3 * T + 4 * S = 50 \)
pricom \(T\) a \(S\) su cele cisla.
Takych dvojic nebude vela.
No a potom mozem spocitat pre kazdu dvojicu \(T\) a \(S\), kolko koliesok mi pre tuto situaciu zostane a najst maximum a minimum.
Mne vyslo ze max. zostane 9 koliesok a min. 2. (ak som sa nepomylil).
Staci takto?
Este dodam, ze ta rovnica
\( 3 * T + 4 * S = 50 \)
je tzv. Diofanticka rovnica (napr. tu: https://cs.wikipedia.org/wiki/Diofantick%C3%A1_rovnice)
Děkuji moc, jen nevím, zda to dobře chápu, našla jsem tyto možnosti ( jde o 5.třídu, tedy ještě nepoužívají rovnice, jen ty nejjednodušší a to až v závěru roku): 32+411 314+42 36+48 310+45
A ten závěr mi nějak nejde. Omlouvám se za natvrdlost, děkuji.
No tak sa pozrime na jedno mozne riesenie, napr. to prve.
Ak pouzijem pri hre strategiu, ze najprv zahram dve trojice a potom jedenast stvoric stvorcekov, celkovo ich pouzijem:
\( 2 * 3 + 11 * 4 = 6 + 44 = 50 \).
Teda som sa zbavil vsetkych stvorcekov, ako bolo v zadani. Ale pre kazdu trojicu stvorcekov musim odobrat styri kolieska. Takisto pre kazdu stvoricu stvorcekov musim odobrat tri kolieska. Teda celkovo odoberiem:
\(2 * 4 + 11 * 3 = 8 + 33 = 41 \)
koliesok. No a kedze som ich mal na zaciatku 50, zostane mi:
\( 50 - 41 = 9 \).
Ked tento vypocet pouzijem pre vsetky mozne dvojice \( T, S \), lahko zistim, kolko mi moze zostat maximalne a minimalne koliesok.
Staci takto?
V ramci 5. tridy bych to resil tak, ze si to budeme kreslit. To je celkem zabavne a taky poucne, protoze kdyz to udelame spravne, najdeme vsechny mozne pozice ve hre.
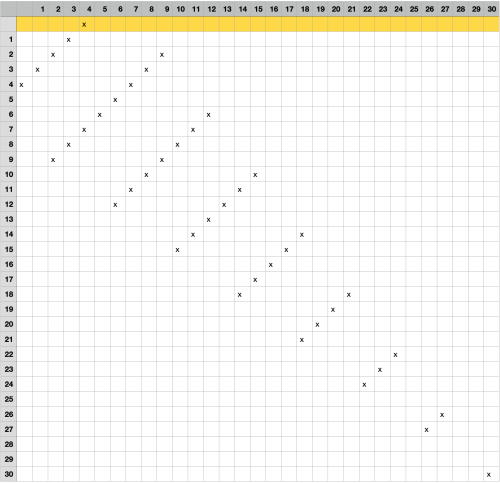
Vezmeme si ctvereckovany papir - nebo tabulku v Excelu ;) - a udelame si tabulku 51x51 a radky i sloupce si ocislujeme od 0 do 50. Cislo radku bude pocet ctverecku, cislo sloupce bude pocet kolecek.
Vpravo dole je pozice oznacena jako 50/50, ktera oznacuje, ze na zacatku mame 50 ctverecku a 50 kolecek. Povolene tahy jsou dva: "3 sloupce doleva, 4 rady nahoru" nebo "4 sloupce doleva, 3 rady nahoru". Vypada to skoro jako skok konem na sachovnici a kazdy krok odpovida tomu, ze jsme nechali zmizet 3 a 4 prvky (nebo 4 a 3 prvky).
Reseni ulohy, kdy nemame zadny ctverecek, odpovida radku 0. Kdyz zacneme tabulku postupne vyplnovat, tak se tam objevi takovy hezky vzor, takze vyplnit to v Excelu je na chvilinku a po doplneni vsech moznych povolenych tahu je hned videt maximum i minimum kolecek, kdyz zmizi ctverecky.
Do prilohy jsem dal screenshot verze, kdy zaciname se 30 kolecky a ctverecky. To je hlavne pro predstavu, jak cele reseni vypada.
Pro kontrolu, puvodni uloha s 50 kolecky a ctverecky by mela mit jen dve reseni, 2 a 9.
Děkuji.