Důvod proč je tenhle trojúhelník rovnostranný
Dobrý den chtěl jsem se poradit jak odůvodnit tenhle příklad.
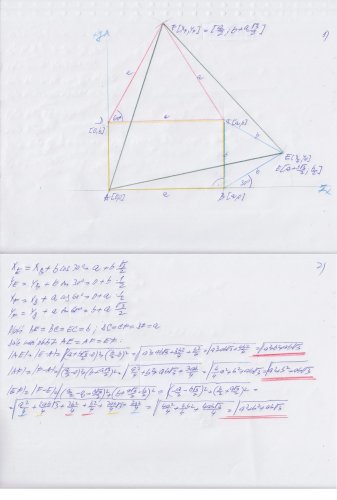
Je dán obdélník ABCD a body E,F tak, že trojúhelníky BEC a CFD jsou rovnostranné a každý z nich má s pravoúhelníkem ABCD společnou pouze stranu .Zdůvodněte, že také trojúhelník AEF je rovnostranný.
Děkuji
Petr J.
23. 02. 2023 17:40
9 odpovědí
Nebo také bez souřadnic např. AF = odmocnina (a^2+b^2-2ab * cos 150°) = odmocnina (a^2+b^2+ab*odmocnina (3)), to samé i AE , stejné délky a,b, stejný úhel 150° proti AE, nebo EF opět stejné délky a,b a stejný úhel 150° proti EF.
Ten druhý způsob byla cosinová věta, tedy strana trojúhelníku AF^2 = EF^2 = AE^2 = a^2 + b^2 * cos 150°, těch 150° dostaneme jako součet pravého úhlu z obdélníku a 60° z přilehlého rovnostraného trojúhelníku.
Dobrý den,
mockrát vám děkuju.
Ahoj,
uvádíš "základní škola" - proto jen doplním, že každou stranu trojúhelníku \(AEF\) lze vypočítat pomocí Pythagorovy věty. Stačí najít příslušné pravoúhlé trojúhelníky.
Nejprve si spočítáš výšky rovnostranných trojúhelníků, např. výška trojúhelníku \(CFD\) je \(\frac{ \sqrt{ 3} } { 2} a\) (pomocí Pythagorovy věty nebo z tabulek).
Dále např. délku strany \(AF\) vypočítáme takto:
Střed strany \(AB\) označím \(X\), vyznačím si pravoúhlý trojúhelník \(AXF\). Odvěsna \(AX=\frac{ a} { 2} \), druhá odvěsna \(XF=b+\frac{ \sqrt{ 3} } { 2} a\). Délku přepony \(AF\) zjistíme pomocí Pythagorovy věty (výsledek uvádí Milan). Dokonce ani nemusíme odmocňovat, jsou-li délky stran shodné, rovnají se i jejich druhé mocniny.
Podobně další dvě strany.
Dobrý den,
děkuji za podrobnější vysvětlení. Jenom co znamená √3:2 a.
(odmocnina ze 3) /2 se tam objeví například proto, že v cosinové větě je AF^2 = a^2 + b^2 - 2 * a * b * cos 150°. Cos 150° = - cos 30°= -(odmocnina 3)/2, a protože tam je -2abcos 150°= + 2ab(odm 3)/2 , bude to kladné. Nebo se tam také objeví proto, že např. strana AF se jako přepona promítá do osy X jako odvěsna, seskládaná z délky strany b a z průmětu strany a pod úhlem 30 °, takže její část je a * cos 30°= a * (odm. 3) /2.
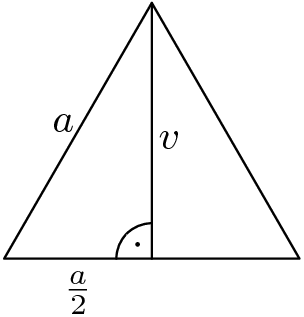
Rovnostranný trojúhelník se stranou \( a \) má výšku \(v=\frac{ \sqrt{ 3} } { 2} a \).
Dá se to odvodit pomocí Pythagorovy věty. Výška rozdělí rovnostranný trojúhelník na dva pravoúhlé trojúhelníky. Jeden pravoúhlý trojúhelník má odvěsnu \(\frac{ a} { 2} \) a přeponu \( a \). Druhá odvěsna je právě hledaná výška.
Podle Pythagorovy věty
\( v^2 + \left(\frac{ a} { 2} \right)^2=a^2\)
a dále postupně
\( v^2=a^2 - \frac{ a^2} { 4} \)
\( v^2=\frac{ 3} { 4} a^2\)
odmocníme
\( v=\frac{ \sqrt{ 3} } { 2} a\)
Mockrát děkuji za vysvětlení.