Dvojný integrál
Zdravím, pocitam dvojny integral (vid obrazok) a snazim sa to riesit transformaciou integralu, len neviem urcit hranice, vedel by niekto pomoct?
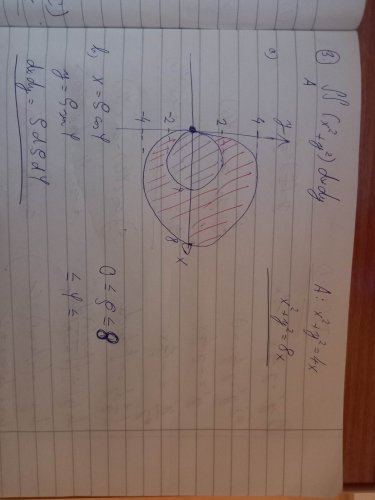
Dvojny integral (x^2+y^2) dxdy
ohraniceny kruznicami: x^2+y^2=4x x^2+y^2=8x
Dakujem
Ján H.
29. 12. 2022 20:10
3 odpovědi
Ahoj,
rozdělil bych to na více částí... takhle:
\(I = \int\int_A \left(x^2 + y^2\right)dxdy = 2\left[\int_{ x=0} ^{ 2} \int_{ y=\sqrt{ 4-\left(x-2\right)^2} } ^{ \sqrt{ 16-\left(x-4\right)^2} } \left(x^2 + y^2\right)dxdy + \int_{ x=2} ^{ 4} \int_{ y=0} ^{ \sqrt{ 16-\left(x-4\right)^2} } \left(x^2 + y^2\right)dxdy \right]\)
Jako druhá možnost mě napadá posunutí úlohy do počátku - \(x \to \left(x+4\right)\) a následně transformace do polárních souřadnic:
\(x = R\cos\varphi,\text{ } y = R\sin\varphi,\text{ } dxdy = RdRd\varphi\)
\( I = \int\int_A \left(x^2 + y^2\right) dxdy = \int_{ R=2} ^4\int_{ \varphi=0} ^{ 2\pi} \left[\left(R\cos\varphi + 4\right)^2 + R^2\sin^2\varphi\right]RdRd\varphi
\)
\( I = \int\int_A \left(x^2 + y^2\right) dxdy = \int_{ R=2} ^4\int_{ \varphi=0} ^{ 2\pi} \left[\left(R\cos\varphi + 4\right)^2 + R^2\sin^2\varphi\right]RdRd\varphi\)