Geometrie - 2 příklady přijímačky : Obvod, Obsah

Přeji pěkné dopoledne, Rostislave,

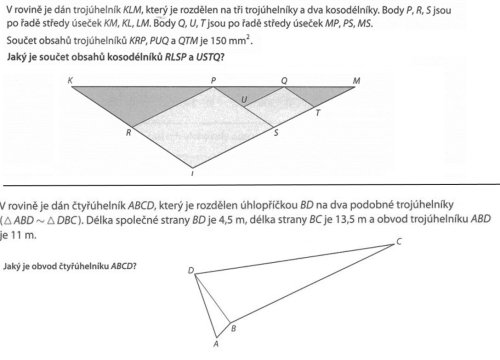
pro začátek je dobré všimnout si toho, že body $P, S, R$ jsou středy stran největšího trojúhelníku $KLM$, tedy usečky $PR, PS, SR$ tvoří střední příčky trojúhelníku $KLM$. Trojúhelník $PSR$ je tudíž příčkovým trojúhelníkem trojúhelníku $KLM$.

Jak známo, střední příčky dohromady rozdělují trojúhelník na čtyři shodné trojúhelníky. To nechám bez důkazu, ale případně jej můžeme nějak dát dohromady, pokud budete chtít.

Smíme tedy prohlásit, že trojúhelníky $KRP, PSR, LSR$ a $PSM$ mají shodný obsah.

Analogicky postupujeme u trojúhelníku $PSM$, jehož příčkový trojúhelník je $QUT$.

Z uvedeného plyne, že kosodélník $USQT$ tvoří polovinu obsahu trojúhelníku $PSM$, tedy obsah trojúhelníku $KPR$ bude dvakrát vyšší než součet obsahů trojúhelníků $PUQ$ a $QTM$.

Víme tedy, že $S(KRP) + S(PUQ) + S(QTM) = 150$ $mm^2$ a současně $S(KRP) = 2 \cdot (S(PUQ) + S(QTM))$.

Snadno tedy odvodíme, že $S(KRP) = \frac{ 2} { 3} \cdot 150 = 100$ $mm^2$.

Z dříve zmíněných informací o příčkových trojúhelnících tedy plyne, že pro hledaný obsah platí:

$S(RLSP) + S(USTQ) = 2 \cdot S(KRP) + \frac{ 1} { 2} \cdot S(KRP) = 250$ $mm^2$.

Pardon, ještě druhý příklad.

Trojúhelníky jsou si podobné, tedy ke každé straně trojúhelníku $CBD$ existuje taková strana trojúhelníku $ABD$, že délky této dvojice stran jsou právě v poměru $1 : k$. Trojice vnitřních úhlů jednoho trojúhelníku je také stejná jako trojice vnitřních úhlů druhého trojúhelníku.

My si z obrázku všimneme, že v poměru $1 : k$ jsou tyto dvojice stran:

$|BD| : |BC| = 1 : k$

$|AB| : |BD| = 1 : k$

$|AD| : |DC| = 1 : k$

Jelikož víme, že platí $|BD| = 4.5$ m a $|CB| = 13.5$ m, pak můžeme odvodit následující:

$|BD| : |BC| = 1 : k$

$4.5 : 13.5 = 1 : k$

$k = 3$

Dále víme, že obvod trojúhelníku $ABD$ činí $11$ m, tedy $o(BCD) = k \cdot o(ABD) = 33$ m.

Z toho plyne, že $|CD| = 15$ m, což plyne z faktu, že známe délky zbývajících stran trojúhelníku $BCD$ o rovněž jeho obvod.

Délky stran $AB$ a $AD$ odvodíme z podobnosti, tedy $|AB| = \frac{ 1} { k} \cdot |BD| = 1.5$ m a $|AD| = \frac{ 1} { k} \cdot |CD| = 5$ m.

Zbývá jen stanovit obvod čtyřúhelníku $ABCD$.

$o(ABCD) = |AB| + |BC| + |CD| + |AD| = 1.5 + 13.5 + 15 + 5 = 35$ m.

Moc Vám děkujeme Tomáši za Vaši pomoc. R