Geomterie

*Geometrie.

Dobrý den, poprosila bych o pomoc, zda byste mi to někdo nenarýsoval a jednoduše nevysvětlil. Děkuji

Ahoj,

komutativita znamená, že mohu operace provést v libovolném pořadí a dostanu stejný výsledek.

Jak v otočení, tak ve středové souměrnosti (ve většině geometrických zobrazení) umíme zobrazovat pouze body, z toho bych vyšel.

Pro definici kruhu potřebuji střed a poloměr, tedy střed a jeden bod na obvodu.

Ještě je potřeba se zamyslet nad tím, že středová souměrnost (i osová) vytvářejí zrcadlové obrazy objektů - překlápí je.

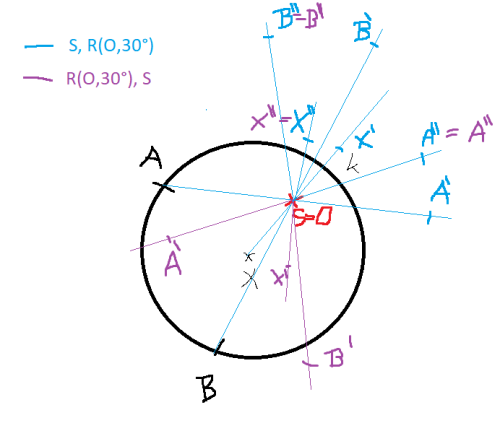
Zobrazíme si tedy střed a dva body na kružnici. Zjistíme, že výsledek je stejný (viz obrázek).

Druhá možnost je na to jít přes definici těchto zobrazení pomocí matic.

Matice rotace kolem počátku soustavy souřadnic je

\(

R(\alpha) = [ [\cos(\alpha), -\sin(\alpha)] , [\sin(\alpha), \cos(\alpha)]] \)

Matice středové souměrnosti se středem v počátku je

\(

S(0,0) = [ [ -1, 0], [0, -1] ]

\)

Aplikace těchto zobrazení se provádí násobením zleva. Násobení matic je asociativní, ale ne komutativní (obecně). Zkus si tyhle matice vynásobit v jednom a druhém pořadí, mělo by vyjít to samé.

Zvolený kruh je komutativní vzhledem k operaci skládání středové souměrnosti a otáčení, pokud platí, že středová souměrnost se provádí kolem středu kruhu a otáčení kolem stejného středu kruhu. V tomto případě je S=O, což znamená, že střed středové souměrnosti je také středem otáčení. Tedy komutativita platí

Zkusme to ukázat na příkladu. Mějme kruh se středem (S) a body (A) a (B) na jeho obvodu:

Středová souměrnost kolem středu kruhu (S):

Středová souměrnost překlápí bod (A) na bod (A’) tak, že (SA = SA’).

Stejně tak překlápí bod (B) na bod (B’) tak, že (SB = SB’).

Otáčení kolem stejného středu kruhu (S) o úhel (\alpha):

Otáčení přesune bod (A’) na bod (A’‘) tak, že úhel (SAA’') je (\alpha).

Stejně tak přesune bod (B’) na bod (B’‘) tak, že úhel (SBB’') je (\alpha).

Nyní zkombinujme tyto operace:

Nejprve provedeme středovou souměrnost a poté otáčení:

(A) se překlopí na (A’) středovou souměrností.

(A’) se poté otáčí na (A’') o úhel (\alpha).

Výsledek je bod (A’').

Naopak, pokud nejprve provedeme otáčení a poté středovou souměrnost:

(A) se otáčí na (A’') o úhel (\alpha).

(A’‘) se poté překlopí na (A’) středovou souměrností.

Výsledek je opět bod (A’').

Tedy v obou případech dostaneme stejný bod (A’'). To znamená, že komutativita platí pro tuto kombinaci středové souměrnosti a otáčení kolem stejného středu kruhu.