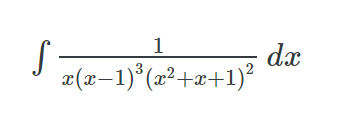Integrace racionální lomené funkce oříšek
Ahoj,
bojuji již delší chvilku s následujícím příkladem a nedaří se mi dosáhnout výsledku. (Něčeho hezkého) Wolfram mi hazí něco nepěkného a rozklad na parciální zlomek je gigantický. :( Poradil by mi prosím někdo jak šikovně na to?
Moc děkuji
Samuel H.
21. 10. 2020 22:24
4 odpovědi
Tady lepší řešení než parc. zlomky nevidím. Akorát pro zlomek se jmenovatelem x můžeš použít zakrývací metodu.
I po rozložení to ale není sranda,musíš poušít ten hnusný rekurentní vzorec pro integrál 1/(x^2+px+q)^n.. no nezávidím ti to, lehký postup ale bohužel asi neexistuje.
V cizině se na tyto kvadráty bez kořenů používá substituce pro integrály obsahující X^2+A^2 substituce x=atan(alfa), ale tady by to s těmi dalšími členy nefungovalo. Nevím proč se v Česku učí ta rekurentní formule a celkově např. Eulerovy substituce pro integrály s odmocninou, když to jde mnohem snáz přes trigonometrické substituce.
Ano, zakrývací metodu jsem použil, ale pro ostatních sedm písmen jsem to zkusil přes inverzní matici a pronásobení vektorem (1,0,0,0..). Nic hezkého. (Invezní mi vypočetl symbolab, ne že bych do ní pustil) Děkuji
Ještě teda,moc to neurychlí, ale i na (x-1)^3 lze použít coverup method.