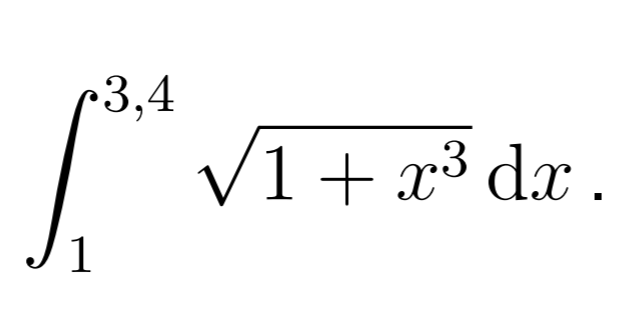Integral

Ahoj Timoteji,

lichoběžníková metoda spočívá v tom, že plochu pod grafem funkce nahradím lichoběžníky a jejich obsahy sečtu.

https://cs.wikipedia.org/wiki/Lichob%C4%9B%C5%BEn%C3…

Interval \( [a,b]=[1;3.4] \) rozdělím na \( n=8 \) shodných dílků o šířce \( 2.4/8=0.3 \).

V bodech \( x_0=a=1, x_1=1.3, x_2=1.6, ..., x_8=b=3.4 \) vypočítám funkční hodnoty \( y_0, y_1, y_2, ..., y_8 \).

Pro usnadnění práce při výpočtu obsahu se používá např. vzorec

\( \displaystyle \int_a^b f(x){ \rm d} x\approx\frac{ b-a} { 2n} (y_0+2y_1+2y_2+...+2y_{ n-1} +y_n) \)

kde tedy \( y_0=f(a), y_n=f(b) \).

Absolutní hodnotu chyby odhadneme podle vzorce

\( \displaystyle \Delta=\frac{ (b-a)^3} { 12n^2} M_2 \)

kde \( M_2 \) je maximální absolutní hodnota 2. derivace funkce \( f(x) \) v intervalu \( [a,b] \).

Výsledky: https://www.wolframalpha.com/input/?i=trapezoidal+rule+from…

Bude-li něco nejasného, rád odpovím.

Keď spravím 2.deriváciu funkcie tak čo dosadim za to M2? Netreba to nejak upraviť?

M2 je maximální hodnota této 2. derivace na intervalu [1; 3,4]. Chyba má vyjít 0,0125.