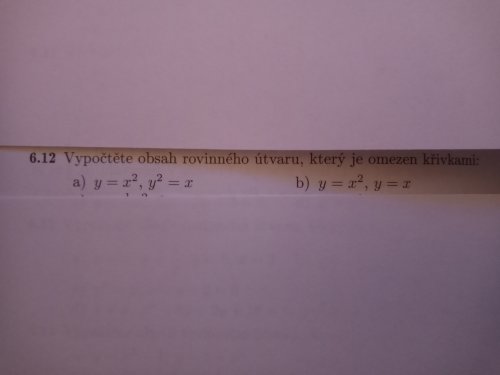Integrál

Ahoj,

Jestli si to správně představuju, tak je to v obou případech ten kousek mezi nulou a jedničkou, jinak bychom měli nekonečnou plochu.

\(S_a = \int_0^1 -x^2 + x^{ \frac{ 1} { 2} } dx = \left[ -\frac{ x^3} { 3} + \frac{ x^{ \frac{ 3} { 2} } } { \frac{ 3} { 2} } \right]_0^1 = -\frac{ 1} { 3} + \frac{ 1} { \frac{ 3} { 2} } = \frac{ 1} { 3} \)

\(S_b = \int_0^1 -x^2 + x dx = \left[ -\frac{ x^3} { 3} + \frac{ x^2} { 2} \right]_0^1 = -\frac{ 1} { 3} + \frac{ 1} { 2} = \frac{ 1} { 6} \)

Dík moc :)