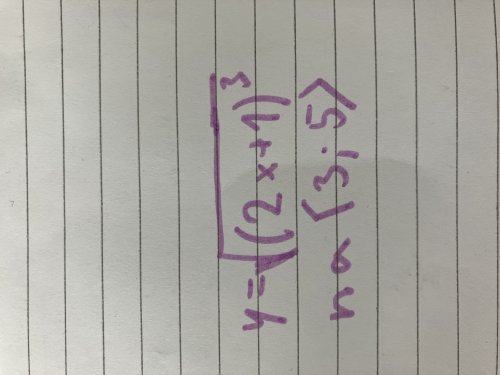Integrály délka křivky

Ahoj, nejdřív si vyjádříme element délky křivky: $dL = \sqrt{ dx^2 + dy^2} = \sqrt{ dx^2 + \left(\frac{ 3} { 2} \sqrt{ 2x+1} \cdot 2 dx\right)^2} = \sqrt{ 18x+10} dx$

a nyní integrujeme:

$\int_3^5 \sqrt{ 18x+10} dx = \left[\frac{ \left(18x+10\right)^{ \frac{ 3} { 2} } } { 27} \right]_3^5 = \frac{ 1000-512} { 27} = \frac{ 488} { 27}$

Viz níže :