Integrály-objem
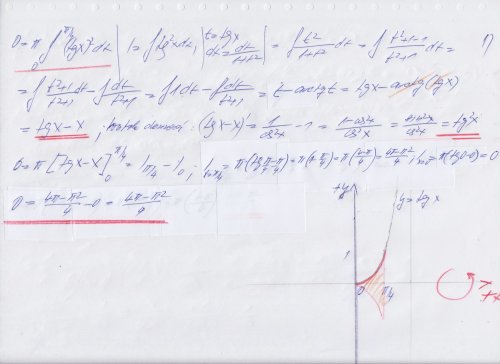
Objem tělesa vzniklého rotací oblasti ohraničené křivkami y=tgx, y=0, x=0,x=pi/4
Předem děkuji za pomoc
Anna K.
06. 06. 2023 16:31
5 odpovědí
Když bude čas, večer se podívám. A také by bylo dobré napsat, kolem které osy to těleso má rotací vzniknout. může vzniknout rotací kolem čehokoliv, ale pak by to nebyl jen jednorozměrný integrál.
No zadání zní přesně takto takto: Vypočítejte objem tělesa vzniklého rotací oblasti ohraničené křivkami y=tg x, y=0,x=0,x=pi/4. Takže netuším další informace k úloze.
Ta substituce byla t = tg x, pak x = arctg t, pak dx je derivace arctg t = dt / ( 1 + t ^ 2 )
Kdyby to mělo být také těleso rotací kolem Y, tak to vede na 2 * pi * integrál x * tg x dx od 0 do pi / 4 a ten bohužel je vyšší transcendentní. Podobně, kdyby se místo tohoto tedy vzala inversní funkce kolem Y, tedy x = arctg y od 0 do 1, tak to bude pi * integrál ( arctg y ) ^ 2 dy od 0 do 1 . šlo by to jen přibližně, nahradit graf tg x lomeným polygonem z úseček tedy lineární funkcí, pak to bude s libovolnou přesností .