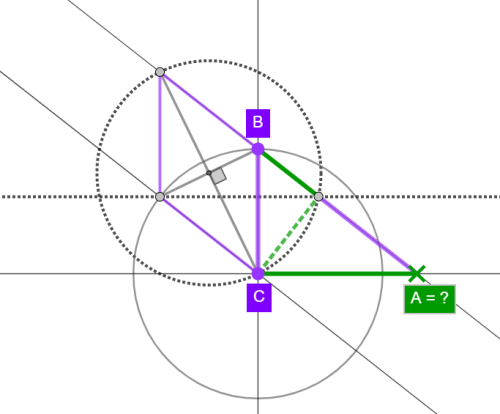
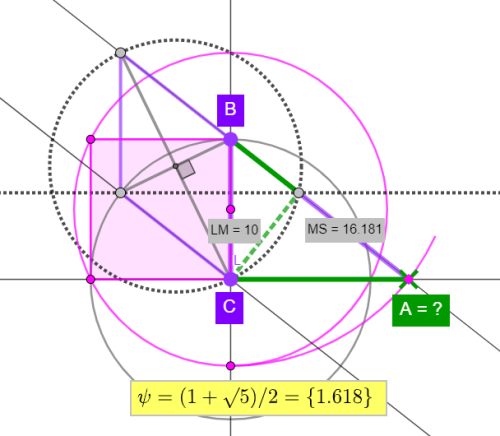
Konstrukce pravoúhlého trojúhelníku
Zdravím. Zasekl jsem se na úloze, kde je dána délka BC a máme sestrojit pravoúhlý trojúhelník ABC, tedy najít vrchol A. Vztahy mezi prvky trojúhelníku a pomocnými prvky jsou jasné z obrázku (pro upřesnění: patou výšky Vc procházejí kružnice se středem v průsečíku výšek kosočtverce a taky přímka rovnoběžná se stranou AC). Uvítám každý nápad ...a pokud konstrukce není eukleidovsky řešitelná, pak jak to lze prokázat.
Petr F.
15. 07. 2021 12:56
5 odpovědí
OPRAVA: ...patou výšky Vc prochází kružnice se středem v průsečíku UHLOPŘÍČEK kosočtverce... (na obrázku je to správně)
Pro upřesnění... ty fialové úseky jsou všechny stejně dlouhé?
Šel jsem na to výpočtem a dostal jsem následující:
\(c_b = a \) - z obrázku
\(v^2 + c_a^2 = a^2\)
\(v^2 + a^2 = b^2 = ca = a(a+c_a) = a^2 + ac_a\)
Z toho dostaneme
\(v^2 = ac_a\) a \(v^2 = a^2 - c_a^2\)
Tedy
\(a^2 - ac_a - c_a^2 = 0\)
\(a = c_a\frac{ 1+\sqrt{ 5} } { 2} \)
Tedy
\(\frac{ a} { c_a} = \frac{ 1+\sqrt{ 5} } { 2} \)
Vzhledem k tomu, že
\(a^2 = cc_a\) tak taky \(\frac{ a} { c_c} = \frac{ c} { a} \)
takže
\(\frac{ c} { a} = \frac{ 1+\sqrt{ 5} } { 2} \)
Poměr stran trojúhelníku tedy tvoří zlatý řez. Teď zbývá vyřešit, jestli jsme tenhle poměr schopni zkonstruovat.
Doufám, že jsem někde neudělal chybku.
Konstrukce zlatého řezu viz https://cs.wikipedia.org/wiki/Zlat%C3%BD_%C5%99ez
Děkuju. Rozhodně zlatý řez, měl jsem z těch proporcí zvláštní pocit ...stačilo si změřit strany.
