Matematika

Ahoj,

obsah kruhu je $S=\pi r^2$, obsah pravidelného osmiúhelníku označím $S_8$. Obsah červeně vybarvené části je $S-S_8$. Chceme zjistit, jaká část kruhu je vybarvena, tedy podíl obsahu červené části a obsahu celého kruhu, neboli

$\displaystyle\quad\frac{ S-S_8} { S}$,

což převedeme na procenta vynásobením 100.

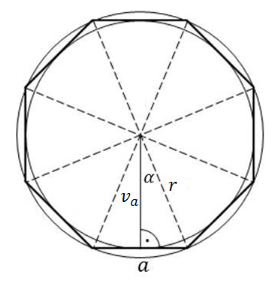
Obsah pravidelného osmiúhelníku vypočítáme takto: Rozdělíme jej na 8 shodných trojúhelníků. Obsah jednoho z nich je

$\quad S_1= \frac{ 1} { 2} av_a$.

Stranu $a$ i výšku $v_a$ potřebujeme vyjádřit pomocí poloměru kružnice opsané $r$. Úhel $\alpha$ snadno dopočítáme z obrázku. Např.

$\displaystyle\quad\sin\alpha= \frac{ a} { 2r} \quad\Rightarrow\quad a=2r\sin\alpha$,

(podobně $v_a$).

Dosadíme do vzorce pro obsah trojúhelníku $S_1$.

Obsah osmiúhelníku je $S_8=8\cdot S_1$.

Nakonec dosadíme do výrazu

$\displaystyle\quad\frac{ S-S_8} { S}$.

Výsledek ještě můžeme upravit pomocí goniometrického vzorce pro $\sin 2\alpha$. Když vyjádříme úhel v radiánech, vyjde docela zajímavý výraz. Číselně mi vychází přibližně 10 % (přesněji 9,97 %).

Dobrý den, Miroslav,

Děkuji moc za odpověď. Počítám už to potřetí a výsledek mi vychází 16,9%.

Tak prosím kontroluj, jestli to mám dobře (nebo můžeš vložit ofocený postup):

$\quad\displaystyle\sin\alpha=\frac{ \frac{ a} { 2} } { r} \quad\Rightarrow\quad a=2r\sin\alpha$

$\quad\displaystyle\cos\alpha=\frac{ v_a} { r} \quad\Rightarrow\quad v_a=r\cos\alpha$

Obsah trojúhelníku

$\quad\displaystyle S_1=\frac{ 1} { 2} av_a=\frac{ 1} { 2} (2r\sin\alpha)(r\cos\alpha)=r^2\sin\alpha\cos\alpha$

Obsah osmiúhelníku

$\quad S_8=8\cdot S_1= 8r^2\sin\alpha\cos\alpha$

Z goniometrie je známý vzorec (v tabulkách)

$\quad 2\sin\alpha\cos\alpha=\sin 2\alpha$

tedy obsah osmiúhelníku je

$\quad S_8 = 4r^2\cdot (2\sin\alpha\cos\alpha)=4r^2\sin 2\alpha$

Z obrázku: $\alpha=(360^\circ/8)/2=22.5^\circ$, tedy

$\displaystyle\quad S_8 = 4r^2\sin 45^\circ=4r^2\frac{ \sqrt{ 2} } { 2}$

Nyní stačí dosadit do výrazu

$\quad\displaystyle\frac{ S-S_8} { S}$

za obsah kruhu $S=\pi r^2$ a za obsah osmiúhelníku.

A když víme, že poloměr kružnice opsané je 7,5 cm, tak šlo by to vypočítat jinak?

Výsledek této úlohy nezáleží na tom, jaký je poloměr ($r$ se nakonec zkrátí). Ať bude obrázek větší nebo menší, poměr obsahu červené části k obsahu celého kruhu bude vždy stejný. Proto si můžeme zvolit třeba $r=1$, ovšem je to dobré zapsat do řešení. Vyšlo to, popř. co není jasné? Můžu doplnit poslední úpravy.

Vyšlo mi 0,316 a jak teďka mám z tohoto čísla vyjádřit kolik to je procent?

Za r jsem dosazovala 1.

Číslo 0,316 je obsah červené části. Potřebujeme zjistit, jaká část kruhu je vybarvená, tj. obsah červené části vydělit obsahem celého kruhu: 0,316/3,14 = 0,10 (přibližně desetina), po násobení stem máme 10 %.

Např. "1 jablko z 5 je červené" můžeme napsat jako 1/5. Podobně zde dáme do čitatele obsah červené části (0,316) a do jmenovatele obsah celého kruhu (3,14).

Můžeme použít i trojčlenku: 100 % ... 3,14 (celý kruh), x % ... 0,316 (červená část).

Děkuji moc