Matematika Mřížový čtyřúhelník

Dobrý den,

obdélník má obsah 12 čtverečků.

A) Označme obsah malého trojúhelníku $m$, velkého $t$ a obsah čtyřúhelníku $c$. Dohromady $m+t+c=12$.

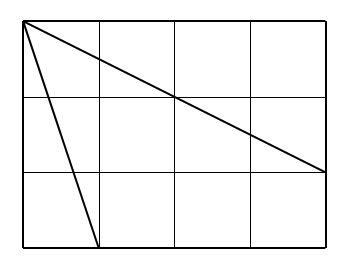
Obsah menšího trojúhelníku tvoří 12,5 % obdélníku (12,5 % ze 12), tj. $m=1{ ,} 5$ čtverečku. Můžeme jej zakreslit jako pravoúhlý trojúhelník se stranami 1 a 3 tak, že stranu délky 3 umístíme jako kratší stranu obdélníku. Obsah tohoto trojúhelníku je $(1\cdot3)/2 =1{ ,} 5$.

Obsah velkého trojúhelníku je aritmetický průměr obsahu malého trojúhelníku a čtyřúhelníku, tedy $t=(m+c)/2$. Dále máme rovnici $m+t+c=12$. Do těchto rovnic dosadíme za $m$ a získáme soustavu dvou rovnic o dvou neznámých $t, c$.

Obsah velkého trojúhelníku vychází $t=4$ čtverečky. Jeho obsah je $(a\cdot v)/2=4$. Zkusíme např. výšku $v=3$ a dopočítáme základnu $a$. Tento trojúhelník může sousedit s malým trojúhelníkem.

Zbytek obdélníku vyplní hledaný čtyřúhelník. Bude-li třeba, rád nakreslím obrázek.

Úlohu B jsem zatím nezkoušel.

Dobrý den, došlo mi, že všechny tři obrazce mají být v čtvercové mřížce, tj. s vrcholy ve vrcholech čtverečků, proto druhý trojúhelník je potřeba umístit podle obrázku (výpočty obsahů jsou správně).

B) Označme obsah menšího trojúhelníku $x$ čtverečků. Větší trojúhelník má obsah $x+0{ ,} 5$ čtverečku.

Obsah čtyřúhelníku se má lišit od obsahu jednoho z trojúhelníků o 1/2 čtverečku, což může být $x, x+1, x+ 0{ ,} 5$ nebo $x- 0{ ,} 5$. Součet obsahů obou trojúhelníků a čtyřúhelníku je 12. Můžeme tedy zapsat čtyři rovnice. Vybereme takové výsledky (obsahy), aby se podařilo trojúhelníky zakreslit do čtvercové mřížky.

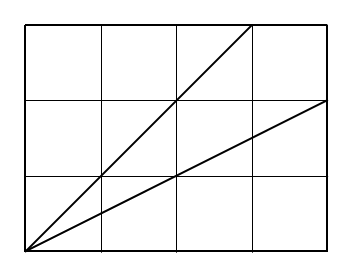
Jednou z možností je obsah čtyřúhelníku $x- 0{ ,} 5$. Součet obsahů dvou trojúhelníků a čtyřúhelníku je $x + (x + 0{ ,} 5)+ (x -0{ ,} 5)=12$, odtud $x=4$. Menší trojúhelník má obsah 4 čtverečky, větší 4,5 čtverečku, čtyřúhelník 3,5 čtverečku. Toto řešení je na obrázku.

Myslím, že schůdné je nejméně ještě jedno další řešení.

Moc děkuju