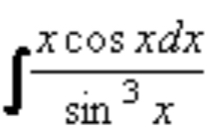Neurčitý integrál - Postup výpočtu

Použitím dvou různých způsobů, protože x a sin x jsou to dosti nesourodé funkce, tak "po částech" alias per partes se zbavit x a pak řešit integrál již bez toho x

Je to velmi jednoduché tak práce na 5 minut.

Viz níže :

Milan, ďakujem za odpoveď a za výpočet. Nanešťastie pre mňa stále nerozumiem.

Píšete, že mám použiť metódu Per Partes. Ako funguje metóda PP viem, viem ako odvodiť vzorec. Čo ma mätie je, že metódou Per Partes sa počíta súčin dvoch funkcii, ale v mojom integráli sú funkcie tri.

Prosím, vysvetlite mi Váš postup.

Ano, ale platí : integrál u´ * v = u * v - integrál u * v ´, přičemž funkcemi "u" i "v" může být cokoliv i součin několika dílčích funkcí " v jednom"

Takže co zlobí v integrálu I , je to x, to jsem označil jako v, potom funkcí u´ bude cos x / sin ^ 3 x. Takže u bude integrál z u´ čili integrál z cos x dx / sin ^ 3 x a to je -1 / ( 2 * sin ^ 2 x ) .Vypočíst jde snadno proto, že mocniny sin a cos jsou liché. Prostě udělá se substituce nějaké t = sin x, pak dt = cos x * dx a to je to celé "nahoře". Potom v ´ je derivace x podle x a to je 1 . A to chceme, protože tím se již x v integrálu nadobro zbavíme. Dále jen pasivně přepíšeme u * v , což je ( -1 / ( 2 * sin ^2 x) ) * x - integrál u * v ´. Ten integrál u * v ´ je integrál u * 1 = integrál u. tedy fakticky to je integrál z předchozího integrálu. Ale to nevadí, protože to je v tu chvíli již jen integrál z ( ( -1 / 2 ) * 1/ sin ^ 2 x ) dx = -1 / 2 * integrál ( 1 / sin ^ 2 x ) dx a ten netřeba řešit, to je přímo tabulkový integrál. Totiž cotg x je primitivní funkcí k němu. A je hotovo. Tak jistě také lze oklikou řešit třeba oklikou přes různé substituce, ale zbytečně a nakonec to dá opravdu cotg x . Ale obvykle se neřeší, protože prostě víme, že derivace cotg x = - 1 / sin ^ 2 x .

Tak mělo tam být minus, protože derivace cotg x = - 1 / sin ^ 2 x . Sice jsem jej minule prokoučoval, ale dvakrát po sobě, takže se zrušilo, v tom níže je to jak má být .

Milan, ďakujem veľmi pekne za ochotu, vážim si to. Už mi je to jasné :)

Tému označujem za vyriešenú.