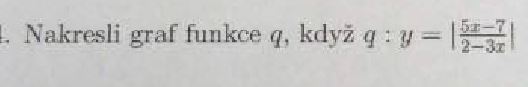Nulové body

Pardon, vložíla jsem špatně příklad.

Ano.

Super, díky. Můžu se zeptat, jak pokračovat? Budu mít 3 intervaly? Nějak se neumím pohnout dál :(

Bod 7/5 je nulový, bod 2/3 je bod nespojitosti funkce.

Ty dva body mi rozdělí definiční obor na tři intervaly. Na prvním a třetím znamená absolutní hodnota změnu znaménka funkce, na prostředním nikoliv.

Pro nakreslení grafu se hodí spočítat limitu v nekonečnech a bodech nespojitosti.

\(\lim_{ x \to -\infty} \left|\frac{ 5x-7} { 2-3x} \right| =\lim_{ x \to -\infty} -\frac{ 5x-7} { 2-3x} = \frac{ 5} { 3} \)

\(\lim_{ x \to +\infty} \left|\frac{ 5x-7} { 2-3x} \right| =\lim_{ x \to -\infty} -\frac{ 5x-7} { 2-3x} = \frac{ 5} { 3} \)

\(\lim_{ x \to \frac{ 2} { 3} ^-} \left|\frac{ 5x-7} { 2-3x} \right| = \frac{ \frac{ 11} { 3} } { \lim_{ x \to \frac{ 2} { 3} ^-} (2-3x)} = \frac{ \frac{ 11} { 3} } { 0^+} = +\infty\)

\(\lim_{ x \to \frac{ 2} { 3} ^+} \left|\frac{ 5x-7} { 2-3x} \right| = \frac{ -\frac{ 11} { 3} } { \lim_{ x \to \frac{ 2} { 3} ^+} (2-3x)} = \frac{ -\frac{ 11} { 3} } { 0^-} = +\infty \)

Dále si můžu spočítat derivaci vnitřní funkce

\(\frac{ d} { dx} \frac{ 5x-7} { 2-3x} = \frac{ 10 - 15x + 15x - 21} { \left(2-3x\right)^2} ,\)

která je všude záporná. Tedy vnitřní funkce je všude klesající. Jelikož mi absolutní hodnota překlápí znaménko funkce, překlápí mi i tuto charakteristiku. Na intervalu do 2/3 se znaménko mění, takže tam je funkce rostoucí. Mezi 2/3 a 7/5 je funkce klesající (v 7/5 je rovna nule) a od 7/5 zase roste.