Objem rotačního tělesa kolem osy x
Vypočtěte objem rotačního tělesa kolem osy x ohraničeného:
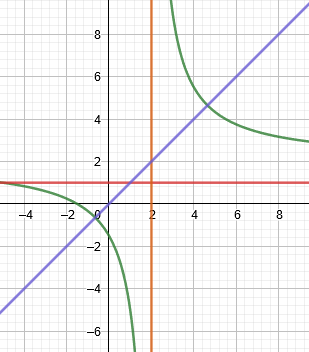
\(y=\frac{ 2x+3} { x-2} , x=2, y=x, y=1\)
V příloze grafy z Geogebry. Která část je takto ohraničená? Nevidím jednoznačnou část roviny, která by takto byla ohraničená.
Michal D.
29. 04. 2021 11:57
K tomuto příspěvku ještě nejsou žádné komentáře.
Buďte první, kdo odpoví!
Buďte první, kdo odpoví!
Pro napsání komentáře se musíte přihlásit.