Podobná zobrazení

1. Jsou možné dva případy: m,n jsou různoběžné, m,n jsou rovnoběžné.

Pro různoběžné leží středy takových kružnic na osách ůhlů sevřených těmito přímkami.

Pro rovnoběžné na ose pásu, který tyto přímky tvoří.

Pak musíme použít ten bod.

V případě rovnoběžek už známe poloměr kružnice, tak si najdeme bod v této vzdálenosti od M na ose pásu a tam bude střed (dvě řešení).

V případě různoběžek potřebujeme ten poloměr najít. Využijeme stejnolehlost.

Narýsujeme libovolnou kružnici se středem na ose úhlu v kvadrantu, kde leží bod \(M\), která se dotýká obou přímek.

Následně spojíme průsečík přímek (střed stejnolehlosti) s bodem \(M\). Tato přímka nám vytvoří dva možné obrazy bodu \(M'\) a \(M"\).

Tyto obrazy spojíme se středem kružnice a následně bodem \(M\) narýsujeme rovnoběžky se vzniklými úsečkami. Tam, kde protnou osu úhlu, budou možné středy výsledné kružnice.

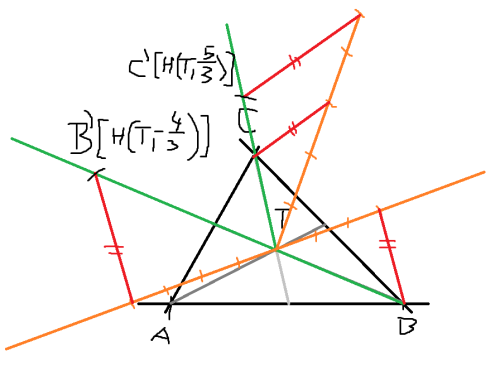
2. Sestrojit trojúhelník pomocí délek všech stran je, předpokládám triviální. Sestrojit těžiště (prúsečík spojnic středů stran a protějších vrcholů) také.

Teď tedy jak na stejnolehlost... Stejnolehlost je rozšířená verze středové souměrnosti. Středová souměrnost je totiž stejnolehlost s koeficientem -1.

Na obrázku je řešení pro verzi a) - bod C a verzi b) - bod B.

V principu postup:

a) Narýsuju přímku, která spojuje zobrazovaný bod a střed stejnolehlosti.

b) Narýsuju libovolnou přímku procházející středem stejnolehlosti, která svírá s tou z bodu a) ostrý úhel.

c) Na přímce z bodu b) vyznačím od středu stejnolehlosti směrem ke zobrazovanému bodu tolik stejných dílků (libovolné, leč rozumné velikosti), jakou hodnotu má jmenovatel koeficientu.

d) Na přímce z bodu b) vyznačím od středu stejnolehlosti tolik dílků (stejně velkých jako v bodu c), jakou hodnotu má čitatel koeficientu.

Pokud je koeficient kladný, značím směrem ke zobrazovanému bodu, pokud je záporný, značím na druhou stranu.

Pozn.: \(2 = \frac{ 2} { 1} \)

e) spojím poslední značku z kroku c) se zobrazovaným bodem.

f) narýsuju rovnoběžku s čarou z kroku e) poslední značkou z kroku d).

g) Tam, kde čára z kroku f) protne spojnici z kroku a), bude obraz bodu.

Ještě ten obrázek...

3. Budeme potřebovat umět sestrojit tečnu z bodu ke kružnici pomocí Thaletovy kružnice.

Pro tečnu z bodu potřebujeme znát bod dotyku. Spojnice středu kružnice a bodu dotyku je kolmá na tečnu (protože tečna je v tomto bodě středu kružnice nejblíže).

Sestrojíme tedy kružnici, která prochází bodem a středem kružnice, ke které děláme tečnu. Její střed bude na spojnici těchto dvou bodů.

Tam, kde nová kružnice protne tu původní, budou body dotyku tečen.

A teď, jak získat ten bod, ze kterého budeme ty tečny rýsovat...

Když si nakreslíme náčrt, všimneme si, že celý obrázek je osově souměrný podle spojnice středů. Navíc si můžeme z podobnosti trojúhelníků dopočítat (věta uuu, usu), že poměr vzdáleností středů kružnic od bodu, kde se tečny protínají, je stejný jako poměr poloměrů těch kruřžnic.

Vidíme tedy, že průsečík tečen bude středem stejnolehlosti, která zobrazuje jednu z kružnic na druhou.

Z předchozí úlohy si vezmeme inspiraci, jak s tím naložit... Narýsujeme kolmice (kvůli snadnému dodržení stejného úhlu, tedy rovnoběžnosti) na spojnici středů kružnic, které budou procházet právě těmito středy.

Tím získáme dvojice bodů, které jsou si vzájemně obrazy. Stačí je tedy spojit a na průsečíku spojnic bude hledaný střed stejnolehlosti.

Pozor! Musíme uvažovat kladný i záporný koeficient, tedy jeden bod bude mezi kružnicemi a druhý vně, za menší z nich.

6. Obraz bodu v osové souměrnosti vytvoříme tak, že narýsujeme kolmici bodem na osu a na druhou stranu od osy naneseme stejnou vzdálenost.

Dále tento obraz potřebujeme posunout. Posunutí provedeme tak, že zobrazovaným bodem narýsujeme rovnoběžku s vektorem posunutí. Následně na ní od zobrazovaného bodu vyznačíme stejnou vzdálenost, jako je délka vektoru posunutí. Tím dostaneme posunutý obraz.

Ad 6) - posunutí se provádí vždy ve směru té šipky