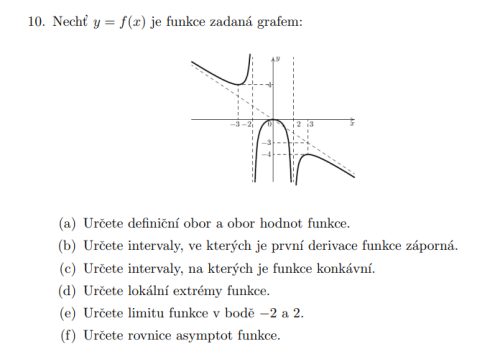
Průběh fce

Ahoj Karle, máš kurz na vyšetřování průběhu funkce? https://mathematicator.com/kurz/vysetrovani-prubehu-funkce

a. Definiční obor i obor hodnot můžeš vyčíst přímo z grafu, který jsi dodal. Zkus ho schválně určit a společně porovnáme řešení. Stačí jen přečíst hodnoty z osy X a Y a správně zapsat intervaly.

d. Jsou tam jenom 3 pro hodnotu -3, 0 a 3

e. Pro -2 je limita zleva a zprava jiná a liší se znaménko u nekonečna. Pro 2 je limita mínus nekonečno

f. Bude to nějaká lineární funkce se záporným znaménkem u X (protože jde dolů), její graf jde dolů. Návod, jak funkci najít je tady: https://mathematicator.com/video/8-predpis-linearni…

Dokážeš vyřešit zbytek věcí už sám? :)

Nejsem si jist, ale ten definiční obor by měl být Df=(-∞;2) U (2;2) U (2; ∞). Je to tak správně ?

Ahoj Karle,

1. definiční obor je \((-\infty;-2) \cup (-2;2) \cup (2; \infty)\), obor hodnot je \(\left(-\infty; 0\right) \cup \left\langle4; \infty\right)\)
2. první derivace je záporná tam, kde je funkce klesající, tedy \((-\infty; -3) \cup (0; 2) \cup (3; \infty)\)

Zbytek už zvládneš?

U toho Df jsem v něktěrých bodech zapomněl napsat znaménko minus, každopádně díky za opravu.

Mám ještě dotaz ohledně tohoto cvičení c) Fce je konkávní na intervalu (-∞; -2) ? a e) Není mi moc jasné jak jste určil tu limitu :( .

1. U konkávnosti si nejsem jistý, ale řekl bych, že je konkávní od (-2; 2) a (2; ∞)
2. Limitu jsem určil podle grafu. Pro hodnotu -2 je zleva +∞ a zprava -∞. Pro hodnotu 2 je -∞ pro obě strany. Je to vidět přímo vizuálně v obrázku, když se podíváš na přímo sousející body nekonečno blízko tomu bodu, tak uvidíš, kam se hodnota funkce blíží.