Rovnoramenné trojúhelníky v rovnoramenném lichoběžníku
Dobrý den, potřeboval bych pomoci s níže uvedeným problémem:
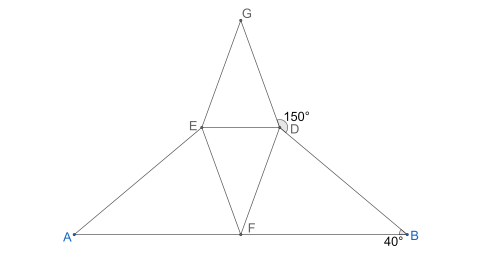
Na obrázku je rovnoramenný lichoběžník ABDE a dva trojúhelníky EDG a EDF, které jsou shodné a rovnoramenné. Délka ramene trojúhelníku EDG je 3,4202 cm a délka jeho základny je 2,3396 cm. \(\measuredangle BDG = 150°\) a \(\measuredangle FBD = 40°\). Bod A' neleží na úsečce AB, ale leží na přímce, která prochází body AB a je od bodu A vzdálena přesně 5 cm. Vypočítejte délku tětivy, na které leží body A'I, kružnice se středem A, jestliže kružnice prochází bodem F a jestliže výška trojúhelníku AA'E na jeho nejdelší stranu je 1,8378 cm a bod I je patou uvedené výšky. (Obrázek je pouze ilustrační)
Děkuji mnohokrát
Otto D.
03. 04. 2022 18:22
2 odpovědi
Obrázek je zde :)
(Vypočítať vzdialenosť A'I je snadné, ale co pak?)
Ahoj,
Jsme schopni dopočítat všechny úhly v obrázku (ze symetrie a pravidel pro trojúhelníky). U vrcholu rovnoramenného je 40 stupňů, u paty ramen je 70 stupňů. Podstatný je úhel A'AE, který bude 140 stupňů.
Jelikož známe úhly, délu horní podstavy a délku ramene trojúhelníků, můžeme vypočítat díky symetrii pythagorovou větou výšku lichoběžníku.
Díky výšce lichoběžníku a úhlu u bodu A můžeme spočítat délku spodní základny (resp. vzdálenost AF, což je poloměr kružnice) - část po úroveň bodu E z funkce tangens, pak přičtu půlku vzdálenosti DE.
Když znám poloměr kružnice a vzdálenost tětivy od středu, můžu pythagorovou větou spočítat její délku (resp. polovinu délky).
Zkus si to takhle rozkreslit.