Rozdělení pozemku

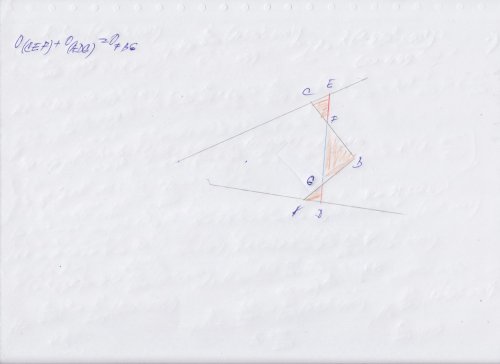
Tak vzhledem k okolnosti, že ty hranice nejsou nijak geometricky a polohově určeny, tak lze říci obecně, že vyrovnávací hranice půjde tedy viz níže : aby plocha FGB se rovnala součtu CEF + ADG. Jenže je vidět, že dotyčný nikdy nedělal geometrické plány pro katastr nemovitostí, ve skutečnosti by pozemky musily být uzavřené a pak by se pokusně udělal třeba bod E, na protější hranici D a pak průsečíky ED CB = F, ED AB = G a spočetly se interaktivně plochy a pokud by to nesedělo, což se nepovede na poprvé nikdy, (ale jsou dost dlouho nicméně k mání programy , kde se dá nová vyrovnávací hranice graficky posouvat a udělat to bez výpočtu) , tak by se vypočetlo, (jde to dost přesně) o kolik je třeba posunout třeba bod E a pak vše znovu, tedy nové průsečíky a znovu plochy a na tři pokusy to bude sedět na 0.01 m ^ 2 , prostě musí to být pod 0.5 m ^ 2 a také s ohledem, jak vycházely výměry včetně zaokrouhlení předtím, aby se vlivem zaokrouhlení nepříhodilo, že se početně jedna zvětší a současně druhá zmenší, musí se kvůli katastrální vyhlášce hlídat spousta věcí, o kterých kdo není UOZI neví.

Ahoj Anno,

na 1. stupni už byste měli znát podobnost trojúhelníků, že?

Podívej se na obrázek v příloze

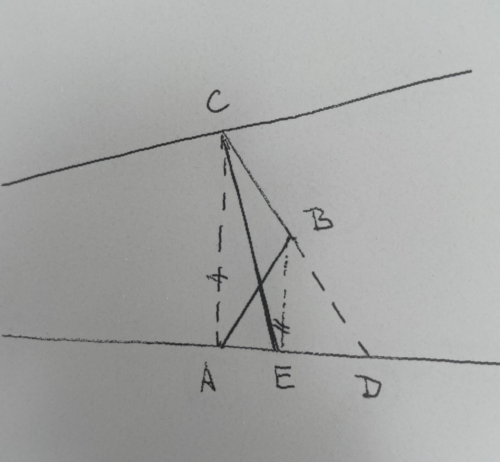
• lomenou čáru označím body ABC

• úsečku BC protáhnu a dostanu bod D jako průnik s hranicí

Teď máme trojúhelník ADC, který představuje "společný" pozemek. Z obou pozemků jsme něco odebrali. Z levého trojúhelník ABC, z pravého trojúhelník ADB.

Poměry jejich obsahů budou stejné, jako je poměr úseček CB a BD. Když se nám povede bod B přenést na úsečku AD ve stejném poměru, máme vyhráno.

Takže z bodu B vedeme přímku BE, která je rovnoběžná s CA a dostaneme, že poměr AE a ED splňuje podmínku.

Úsečka CE je nové dělení pozemků, které zachová rozlohu.

Ještě mi došlo, že to zbytečně komplikuju :)

Stačí si uvědomit, že obsah trojúhelníku je daný stranou a výškou. Když máš trojúhelník ABC určený lomenou čarou a sestrojíš BE rovnoběžnou s AC, bude obsah trojúhelníku ABC stejný jako obsah AEC. Takže CE je nová hranice.